위성의 자세는 어떤 특정 Frame에서 위성이 얼마나 회전했는지를 통해서 나타낸다. 즉 다시 말하자면 위성의 Frame 회전으로 위성의 자세를 표현한다. 그러다보니 어떤 기준 좌표계 A(Reference Frame)으로부터 회전하여 위성의 Frame이 결정된다고 이야기 할 수 있다.
그전에 어떤 기준 좌표계와 같은 경우에는 천문에서 많이 쓰는 좌표계를 사용한다. 그러면 위성이 어떤 Attitude로 있는지 알기 위해서는 A에서 B로 가는 Frame 전환을 해주면 알 수 있다. 따라서 Attitude는 이러한 변환을 통해서 Attitude를 나타낸다. 매우 많은 변환이 있지만 대표적으로 3가지를 다루고자 한다.
- DCM(Direction Consine Matrix)
- Euler Angle
- Quaternion
DCM
DCM은 두 Frame 사이의 차이대로 변환을 시켜주는 방법이다. 다음과 같이 변환 행렬이 존재하는데, 3차원이라고 가정하면 총 3개의 orthnormal한 Frame을 가정할 수 있다. 이러한 3개의 orthonomal vector로 만들어지는 두 Frame사이의 변환을 도와주는 Matrix라고 생각하면 된다. 이 행렬에 B Frame에서의 벡터를 넣으면, A Frame에서의 백터로 바꾸어준다. 따라서 실제로 위성의 Attitude를 표현하는 방법이다. 여기서 아래에 있는 식은 Active DCM이다.

Passive DCM: Passive DCM은 벡터가 포함되어 있는 Frame이 옮겨지는 개념이다.
Active DCM: Active DCM은 벡터 자체가 다른 Frame으로 옮겨가는 개념이다.
Passive DCM과 Active DCM은 서로 역관계에 있는데 det가 1이므로, Transpose 관계이기도 하다.
Euler Angles
Euler angles는 각 Axis를 돌려서 변환시키는 것을 의미한다. 따라서 총 3축에 대해서 회전하므로 R1, R2, R3가 있다. 이때, 시작과 끝이 같더라도 중간 과정이 같을수도 있다. 그래서 한번에 같은 것을 옮기는 경우를 제외하면 총 3x2x3 = 12가지 경우로 표현이 가능하다. 그러다보니 일반적으로 3-2-1순서로 회전하는 것을 많이 사용한다.
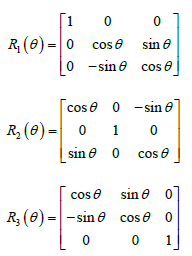
Quaternion
Quaternion은 어떤 축에 대해서 회전하는 변환관계를 나타낸다고 이해하면 된다. 따라서 축을 나타내기 위한 백터와 그리고 회전 각도를 나타낸다. 따라서 총 4개의 요소를 가진다. 이는 Euler Angle과 같이 직관적이지 않아서 따로 설명하기는 어렵지만, 이 3가지 표현 방법의 변환이 가능하여서 계산 과정에서는 가장 장점이 많은 Quaternion을 사용한다.


Transformation
Quaternion to DCM
이도 매우 중요하다. 기본적으로 quaternion이 일반적으로 위성의 Attitude를 나타내는데 이용하는데, 이 quaternion으로는 실제 어떻게 있는지 파악하기 어렵기 때문에 DCM으로 변경해서 위성의 Attitude를 파악한다.

Euler Angles to quaternion
Euler Angle을 quaternion으로 바꿔주는 것은 어렵지 않다. 아래에 있는 식을 이용해서 변환해주면 된다. 이때, Roll이 pi, Pitch가 theta, yaw가 csi이다.

'작은 공부방' 카테고리의 다른 글
| Project - 위성의 궤도 plot 프로그램 (2) | 2022.07.19 |
|---|---|
| sgp4와 수치적분을 이용한 위성 시뮬레이션 코딩 (8) | 2022.07.11 |
| System Modeling: Euler's equation(rigid body) (0) | 2022.07.06 |
| Astropy.coordinates Library (0) | 2022.07.04 |
| Earth-centered inertial(ECI) Coordinte Frame (2) | 2022.07.04 |



