Introduction
이전에 배웠던 내용은 크게 2가지로 나눌 수 있다. 위성
- 위성의 위치
- 위성의 자세
첫 번째는 위성의 위치이다. 위성의 위치는 Simplified pertubation models의 한 종류인 sgp4를 이용해서 모사하였다. 이 알고리즘을 이용하면 TLE 데이터를 이용해서 Julian date에 따른 위성의 위치 정보를 반환한다. 따라서 이를 토대로 특정 시간에 위성의 위치를 파악할 수 있다.
두 번째는 위성의 자세이다. DCM은 특정 벡터를 다른 좌표계에서의 벡터로 바꾸어주는 행렬이다. 이를 토대로 위성의 자세를 모사할 수 있는데, 실제 우리가 위성에서 측정할 수 있는 값은 위성의 각속도 값이다. 그래서 위성의 각속도를 통해서 위치를 파악해야하는데, quaternion은 이를 가능하게 한다. 따라서 quternion을 수치적분으로 구한 후 이를 토대로 위성의 위치를 파악할 수 있다.
Implementation
첫 번째로 위성의 궤도이다. 위성의 궤도는 파이썬의 sgp4 모듈을 이용하면 쉽게 구할 수 있다. 이때 주의해야할 점이 있다. sgp4는 기본적으로 TEME 좌표계에서의 위치를 반환한다. 하지만 실제로 이 TEME 좌표계는 시간에 따라서 좌표계가 바뀌는 특징이 있어서 위성의 궤도를 모사하기에 적합하지 않다. 또한 일반적으로 쓰이는 좌표계는 ICRS이므로, 이로 좌표계를 변환해주는 과정이 필요하다. 따라서 다음과 같이 sgp4 모듈로 구한 궤도 정보를 julian date를 이용해서 모두 ICRS로 변환해주었다. 이를 바탕으로 ICRS 좌표계에서 julian date에 따른 위성의 위치를 계산한다.
sat_path = orbit(sat_list[target_sat], jd, fr)
juliandate = [x+y for x, y in zip(jd, fr)]
for ele, juli in zip(sat_path,juliandate):
xc, yc, zc = ele
new_cord = SkyCoord(x = xc, y = yc, z = zc, frame = TEME(obstime = Time(juli,format = 'jd')), unit = 'kpc' , representation_type = 'cartesian').transform_to('icrs')
new_cord.representation_type = 'cartesian'
sat_new_path.append([new_cord.x.value, new_cord.y.value, new_cord.z.value])
두 번째는 위성의 자세이다. 위성의 자세는 DCM으로 표현이 되는데, DCM으로 직접 계산하는 것 보다 여러가지 장점이 있는 quaternoion을 이용해서 계산한다. 이 때, quaternion은 각속도에 따라서 변화하는데, 이 계산 식은 다음과 같다. 따라서 각속도를 알고 있다면 계산할 수 있는데, 이 각속도는 센서에 의해서 측정될 수도 있고, 외부 토크와 초기 각속도 정보를 이용한 수치적분으로도 구할 수 있다.
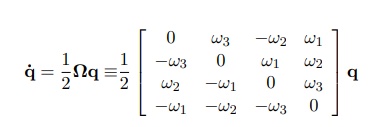
여기서 w1, w2, w3는 3축의 각속도 정보라고 보면 된다. 초기 quaternion을 알고 있다면, 특정 지점의 quaternion 변화량을 계산할 수 있으며, 수치 적분을 이용해서 다른 시간의 quaternion을 계산할 수 있다. 아래의 코드에서는 각속도 또한 수치적분을 이용해서 계산하였다.
def f_v(t, w):
trans_w = np.transpose(w)
trans_h = np.transpose(I@w)
res = np.cross(trans_w, trans_h)
return I_inv@(M(t) - np.transpose(res))
def f_q(t, q, w):
w1, w2, w3 = np.transpose(w)[0]
omega = np.array([[0, w3, -w2, w1],
[-w3, 0, w1, w2],
[w2, -w1, 0, w3],
[-w1, -w2, -w3, 0]])
def rungekutha(t, w, q, h):
k1 = h * f_v(t, w)
k2 = h * f_v((t+h/2), (w + k1/2))
k3 = h * f_v((t+h/2), (w + k2/2))
k4 = h * f_v((t+h), (w + k3))
new_w = w + (k1 + 2*k2 + 2*k3 + k4) / 6
k1 = h * f_q(t, q, w)
k2 = h * f_q((t+h/2), (q + k1/2), w)
k3 = h * f_q((t+h/2), (q + k2/2), w)
k4 = h * f_q((t+h), (q + k3), w)
new_q = q + (k1 + 2*k2 + 2*k3 + k4) / 6
return new_w, new_q한 가지 더 유의할 점은 spg4는 julian date로 시간을 표현하므로, 이 julian date와 일반 시간 사이의 time scale을 맞추는 과정이 필요하다. 이 부분은 datetime을 이용해서 해결해주었다. 실제로 위성의 움직임이 엄청나게 빠르지는 않으므로 1초를 기준으로 하여서 구현하였다.
def make_jd(start_date, duration_time):
jd_li, fr_li = [], []
for i in range(duration_time):
new_day = start_date + timedelta(seconds = i)
yr, mon, day = new_day.year, new_day.month, new_day.day
hour, min, sec = new_day.hour, new_day.minute, new_day.second
jd, fr = jday(yr, mon, day, hour, min, sec)
jd_li.append(jd)
fr_li.append(fr)
return np.array(jd_li), np.array(fr_li)이후 이를 애니메이션을 이용해서 표현하였다. 그 외에 자세한 부분은 아래 코드 파일을 확인하면 된다.
Result
다음과 같은 코딩을 통해서 구현된 결과물은 다음과 같다. 이때 TLE 데이터는 우주정거장의 데이터를 사용했으며, julian date도 임의의 날짜를 사용하였다. 따라서 이 움직임이 큰 의미가 있지는 않지만, 실제로 해당 데이터를 이용한다면 유의미한 궤도 시뮬레이션을 진행할 수 있을 것으로 기대한다.
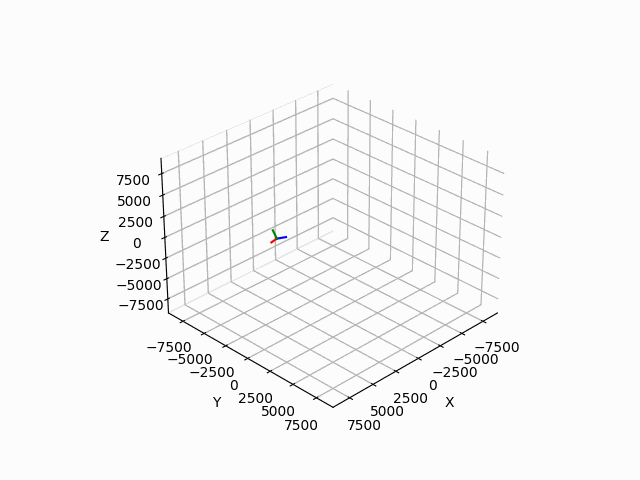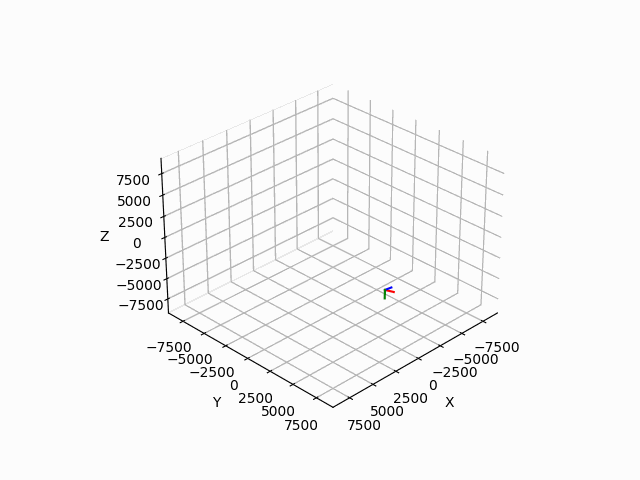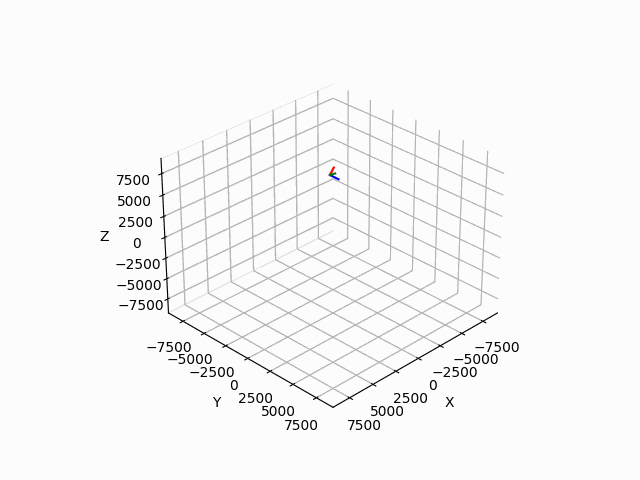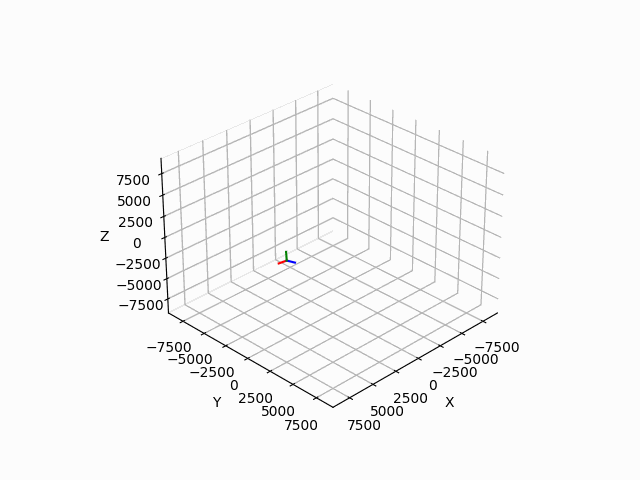
'작은 공부방' 카테고리의 다른 글
| GNSS/INS Integration with Kalman Filter (1) (0) | 2024.03.20 |
|---|---|
| Project - 위성의 궤도 plot 프로그램 (2) | 2022.07.19 |
| Attitude and Frame (0) | 2022.07.07 |
| System Modeling: Euler's equation(rigid body) (0) | 2022.07.06 |
| Astropy.coordinates Library (0) | 2022.07.04 |



